OpenGL-ben és WebGL-ben a csúcspontokhoz rendelhetünk normálvektort, az X-, Y- és Z-komponensük megadásával.

Érdekes módon a Three.js ezen túl bevezeti a lapnormál fogalmát is. A program futásakor ezekből generálja le a normálvektor tömböket. A normálvektorokat a Face3 objektumnak kell átadni.

A normálvektorokat általában nem "kézzel" adjuk meg, hanem felhasználjuk a Three.js segédfüggvényeit. Ha külső modellező programot használunk a geometria létrehozásához (pl. Blender, lásd a következő anyagrészben), az gondoskodik a megfelelő normálvektorokról.

Lapnormálok számítása

A három csúcspont által kifeszített sík normálvektorát állítja be a laphoz, figyelembe véve az előlap irányát. Minden lapra elvégzi a számítást.

Ez a jó megközelítés, ha hangsúlyozni szeretnénk, hogy a felszín különálló lapokból áll, vagy ha a lapok által bezárt szög nagy (vagyis közel sincsenek egy síkban).

geometry.computeFaceNormals();

Csúcspontokhoz tartozó normálok számítása

Ehhez szükséges, hogy előzetesen a lapnormálok meg legyenek határozva. Mivel egy csúcspont több lap része is lehet, a csúcsponthoz tartozó lapnormálok átlagát fogja venni. Beállítható, hogy az átlagolás a síkidom területek arányában történjen-e (a kis területhez tartozó "ne húzza el").

Akkor érdemes használni, ha a lapokkal íves felszínt közelítünk, és nem szeretnénk, ha a szomszédos lapok láthatóan elkülönüljenek.

geometry.computeVertexNormals(); // Területi átlagolás az alapértelmezés

További változatok:

geometry.computeVertexNormals( true ); // Területi átlagolással
geometry.computeVertexNormals( false ); // Normálvektorok egyszerű átlagolása

Területi átlagolás magyarázat (forrás: Lighthouse3d.com):

A Three.js segéd geometriákat biztosít a lapnormálok és a csúcspont normálok megjelenítéséhez. Ez hasznos a nyomkövetéskor, ha ellenőrizni szeretnénk, hogy a normálvektorok megfelelően beállításra kerültek-e? Egy már létrehozott felszínhálóhoz kell rendelni őket.

Lapnormál megjelenítése

fNH = new THREE.FaceNormalsHelper( mesh );
mesh.add( fNH );

Csúcspont normálok megjelenítése

vNH = new THREE.VertexNormalsHelper( mesh );
mesh.add( vNH );

Körlap közelítést végzünk szabályos N-oldalú sokszöggel. A modellezés különféle paramétereit interaktívan kapcsolhatjuk. Látható, hogy a normálvektorok megadásával a reflektor megvilágítás hatása szépen érvényesül.

Tanulmányozzuk át a forráskódot, nézzük meg, hogyan kezeljük a sugár (R) és oldalszám (N) paraméter változásokat!

A megoldás (ThreeJsCircleExample) megnyitható önálló oldalon is.

Bár erre jellemzően nincs szükségünk, a teljesség kedvéért megmutatjuk, manuálisan hogyan definiálhatók a normálvektorok.

Laphoz tartozó normálvektort az alábbi módon adhatjuk meg.

var face = new THREE.Face3( 0, 1, 2 );
face.normal.set( 0, 0, 1 );
geometry.faces.push( face );

Ha a három csúcsponthoz egyenként adnánk meg, akkor a Face3.vertexNormals tömbjét használhatjuk. Természetesen ekkor akár három különböző irányt is megadhatunk, bár a példánkban ugyanaz szerepel.

var face = new THREE.Face3( 0, 1, 2 );
face.vertexNormals[0] = new THREE.Vector3( 0, 0, 1 );
face.vertexNormals[1] = new THREE.Vector3( 0, 0, 1 );
face.vertexNormals[2] = new THREE.Vector3( 0, 0, 1 );
geometry.faces.push( face );

Hogyan állapítsuk meg a normálvektort?

• Ha a síkidom valamelyik fősíkon (pl. XY) helyezkedik el, akkor a harmadik tengely iránya lesz az (figyelembe véve a síkidom előlap irányát).
• Ha általános helyzetű a síkidomunk, akkor a három csúcspont térbeli koordinátái meghatároznak egy síkot, aminek ki tudjuk számítani a normálvektorát és ezt használhatjuk.

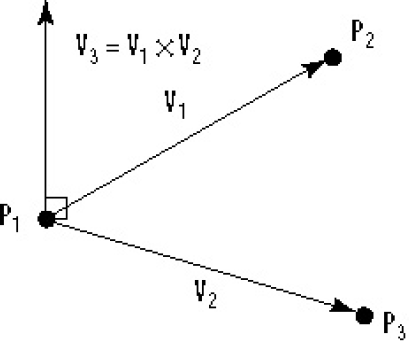
Normálvektor számítása háromszögre

P₁, P₂, P₃ csúcspontokból V₁ és V₂ vektort képzünk, majd vesszük V₁ és V₂ keresztszorzatát. Ennek egy eredménye egy olyan vektor, amely az előző kettőre merőleges irányú. Az egységnyi hosszúságot úgy kapjuk, hogy V₃ komponenseit elosztjuk V₃ hosszával. V₃ hosszát pedig a komponenseinek négyzetösszegéből vont négyzetgyökként kapjuk (Euklideszi távolság az origótól).

Three.js Geometry.js forráskód részlet.

computeFaceNormals: function () {
    var cb = new THREE.Vector3(), ab = new THREE.Vector3();
    for ( var f = 0, fl = this.faces.length; f < fl; f ++ ) {

        var face = this.faces[ f ];

        var vA = this.vertices[ face.a ];
        var vB = this.vertices[ face.b ];
        var vC = this.vertices[ face.c ];

        cb.subVectors( vC, vB );
        ab.subVectors( vA, vB );
        cb.cross( ab );

        cb.normalize();

        face.normal.copy( cb );
    }
}

Three.js Vector3.js forráskód részlet.

subVectors: function ( a, b ) {

    this.x = a.x - b.x;
    this.y = a.y - b.y;
    this.z = a.z - b.z;

    return this;
}

cross: function ( v ) {
    var x = this.x, y = this.y, z = this.z;

    this.x = y * v.z - z * v.y;
    this.y = z * v.x - x * v.z;
    this.z = x * v.y - y * v.x;

    return this;
}

normalize: function () {
    return this.divideScalar( this.length() );
}

length: function () {
    return Math.sqrt( this.x * this.x + this.y * this.y + this.z * this.z );
}