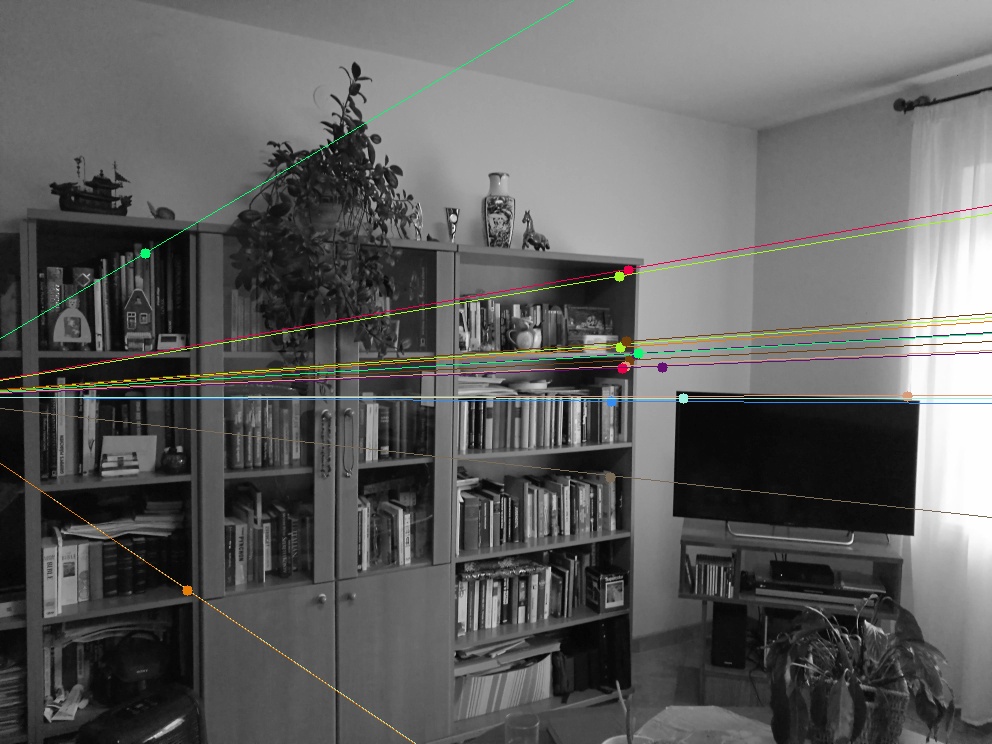
A fundamentális mátrix számításához a két képen potenciális AKAZE kulcspont-párokat keresünk a korábban megismert módon.

A korábbi síkhomográfiát feltételező RANSAC algoritmus helyett az epipoláris geometriai kényszert alkalmazzuk a pontpárok szűrésére. Az inlier pontok alapján megtörténik a fundamentális mátrix meghatározása is.

Meghatározzuk és kirajzoljuk a kulcspontokat és a párjukhoz tartozó epipoláris egyeneseket. Jól látható, hogy az ugyanazon színnel ábrázolt pontokon mennek át az egyenesek.

#
# Based on
# https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_calib3d/py_epipolar_geometry/py_epipolar_geometry.html
#

import cv2
import numpy as np

MIN_MATCH_COUNT: int = 10

img1Name = 'room_scene1.jpg'
img2Name = 'room_scene2.jpg'

def drawlines(img1, img2, lines, pts1, pts2):
    ''' img1 - image on which we draw the epilines for the points in img2
    lines - corresponding epilines '''
    r, c = img1.shape
    img1 = cv2.cvtColor(img1, cv2.COLOR_GRAY2BGR)
    img2 = cv2.cvtColor(img2, cv2.COLOR_GRAY2BGR)
    cidx = 0
    for r, pt1, pt2 in zip(lines, pts1, pts2):
        # color = tuple(np.random.randint(0, 255, 3).tolist())
        color = colors[cidx % 10]
        cidx = cidx + 1
        x0, y0 = map(int, [0, -r[2]/r[1]])
        x1, y1 = map(int, [c, -(r[2]+r[0]*c)/r[1]])
        img1 = cv2.line(img1, (x0, y0), (x1, y1), color, 1)
        img1 = cv2.circle(img1, tuple(pt1), 5, color, -1)
        img2 = cv2.circle(img2, tuple(pt2), 5, color, -1)
        return img1, img2

 

np.random.seed(10)
colors = []
for i in range(0, 10):
    colors.append(tuple(np.random.randint(0, 255, 3).tolist()))

img1 = cv2.imread(img1Name, 0)  # baseImage
img2 = cv2.imread(img2Name, 0)  # queryImage
img2_gr_bgr = cv2.merge((img2, img2, img2))

# Initiate detector
kpextract = cv2.AKAZE_create()
# kpextract = cv2.ORB_create()

# Find the keypoints and descriptors
kp1, des1 = kpextract.detectAndCompute(img1, None)
kp2, des2 = kpextract.detectAndCompute(img2, None)

print('Keypoints in img1:', len(kp1))
print('Keypoints in img2:', len(kp2))
img1kp1 = cv2.drawKeypoints(img1, kp1, None, (255, 0, 0), 4)
img2kp2 = cv2.drawKeypoints(img2, kp2, None, (255, 0, 0), 4)

# Matching based on descriptor similarity
# HAMMING should be used for binary descriptors (ORB, AKAZE, ...)
# NORM_L2 (Euclidean distance) can be used for non-binary descriptors (SIFT, SURF, ...)
matcher = cv2.BFMatcher(cv2.NORM_HAMMING)
matches = matcher.knnMatch(des1, des2, 2)

# Number of matches will be the number of keypoints in img1
print('Matches found: ', len(matches))

# Store all the good matches using Lowe's ratio test.
good_match = []
match_ratio = 0.7
pts1 = []
pts2 = []
for m, n in matches:
    if m.distance < match_ratio * n.distance:
        good_match.append(m)
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)

print("Potential good matches found:", len(good_match))

# Computing correspondences
if len(good_match) < MIN_MATCH_COUNT:
    print("Not enough matches are found - %d/%d" % (len(good_match), MIN_MATCH_COUNT))
    exit(1)

pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
F, mask = cv2.findFundamentalMat(pts1, pts2, cv2.FM_LMEDS)
print(F)
print(np.linalg.matrix_rank(F))

# We select only inlier points
pts1 = pts1[mask.ravel() == 1]
pts2 = pts2[mask.ravel() == 1]

print('Used number of point pairs:', len(pts1))

# Find epilines corresponding to points in right image (second image) and
# drawing its lines on left image
lines1 = cv2.computeCorrespondEpilines(pts2.reshape(-1, 1, 2), 2, F)
lines1 = lines1.reshape(-1, 3)
img5, img6 = drawlines(img1, img2, lines1, pts1, pts2)

# Find epilines corresponding to points in left image (first image) and
# drawing its lines on right image
lines2 = cv2.computeCorrespondEpilines(pts1.reshape(-1, 1, 2), 1, F)
lines2 = lines2.reshape(-1, 3)
img3, img4 = drawlines(img2, img1, lines2, pts2, pts1)

cv2.imshow('ep1', img5)
cv2.imshow('ep2', img3)

cv2.waitKey(0)
cv2.destroyAllWindows()

Eredmények a room_scene képpáron.

Az inlier pontpárok és a fundamentális mátrix ismeretében mindkét képre meghatározható egy-egy síkhomográfia, amely az epipoláris egyeneseket vízszintes irányba hozza úgy, hogy az egymásnak megfelelő vonalak a két képen ugyanazon rasztersoron helyezkednek el. Ez megfelel egyébként a párhuzamos vetítési irányú és megegyező vetítési síkkal rendelkező sztereó kamerapárnak.

A stereo_epipolar_rectify.py példaprogram érdemi új része mindössze az alábbi. A cv2.stereoRectifyUncalibrated() függvény által visszaadott síkhomográfia mátrixokat alkalmazzuk a képekre a cv2.warpPerspective() függvénnyel.

# Compute rectifying homographies
retval, H1, H2 = cv2.stereoRectifyUncalibrated(pts1, pts2, F, (w, h))

img1H1 = cv2.warpPerspective(img1, H1, (w, h))
img2H2 = cv2.warpPerspective(img2, H2, (w, h))

Eredménye a room_scene képpárra (az eredményképet felére kicsinyítve a jobb láthatóság miatt):

Párhuzamos vetítési irányok, vagy rekfikált képpárok esetén a vízszintes rasztervonalak mentén meghatározhatjuk az egyes képpontok párját a másik képen. A párok X-koordinátáinak különbsége jellemzi, hogy a térbeli pont milyen messze van a kamerák közös koordináta-rendszerének origójától. Közelebbi objektumpontok esetén a diszparitás érték nagyobb, míg elegendően nagy távolság esetén nagyjából ugyanarra a koordinátára esnek a két képen.

Megjegyezzük, hogy a diszparitás érték nem lineáris! Vagyis például kétszer akkora diszparitás érték nem kétszeres távolságot jelent.

Az OpenCV az úgynevezett blokkillesztéses algoritmust valósítja meg diszparitás (mélység) térkép számításhoz. A stereo_depthmap.py példaprogram mutatja be a használatát. Létre kell hoznunk egy StereoBM objektumot, aminek utána meghívhatjuk a compute() függvényét. Bementként rektifikált képeket vár!

stereo = cv2.StereoBM_create(numDisparities=64, blockSize=15)
disparity = stereo.compute(imgL, imgR)
disparity = cv2.normalize(disparity, None, 0, 255, cv2.NORM_MINMAX, cv2.CV_8UC1)

Működése a KITTI adatbázis egy sztereó képpárjára az alábbi.

Bal és jobb oldali kamera képek:

A generált mélységtérképen a világosabb pontok jelölik a közelebbi objektumokat. Fekete az a rész, ahol az algoritmus nem talált megfeleltetést, így nem tudott diszparítást számolni.

Amennyiben a kamerák belső kalibrációs paramétereit ismerjük (vagyis ismerjük a kamerák látószög-tartományát, azaz minden képponthoz hozzá tudunk rendelni egy térbeli irányt), akkor a 2D képpontot vissza tudjuk vetíteni 3D térbe mindkét kamera képéről. A félegyenesek metszéspontja megadja a térbeli pont helyét. (A gyakorlatban nem feltétlenül történik meg a tényleges metszés, de választhatjuk például a hozzájuk legközelebbi pontot.) Az ehhez szükséges kamera kalibrációval és a térbeli háromszögeléssel itt nem foglalkozunk.