A program indulás ebben az esetben is a main függvény.

A main felépítése hasonlít a korábbi megoldás GPU-s változatához, de egyszerűbb annál. például az adatok byte->float konverziója megoldható egy for ciklussal, nem kell neki külön függvényt írni.

    for(i=0; i<w*h*4; i++) {
        temp_src[i] = image[i];
    }

Az iteratív számítás, is hasonlóan történik, mint korábban, csak annál egszerűbben.

    for(i=0; i<1000; i++) {
        if(i%2) {
            smoothOnCPU(temp_src, temp_dst, w, h);
        } else {
            smoothOnCPU(temp_dst, temp_src, w, h);
        }
    }

És végül a visszakonvertálás és a kiírás is egyszerűsödik.

    for(i=0; i<w*h*4; i++) {
        image[i] = temp_src[i];
    }

    writeRGBImageToFile("out.png", image, w, h);

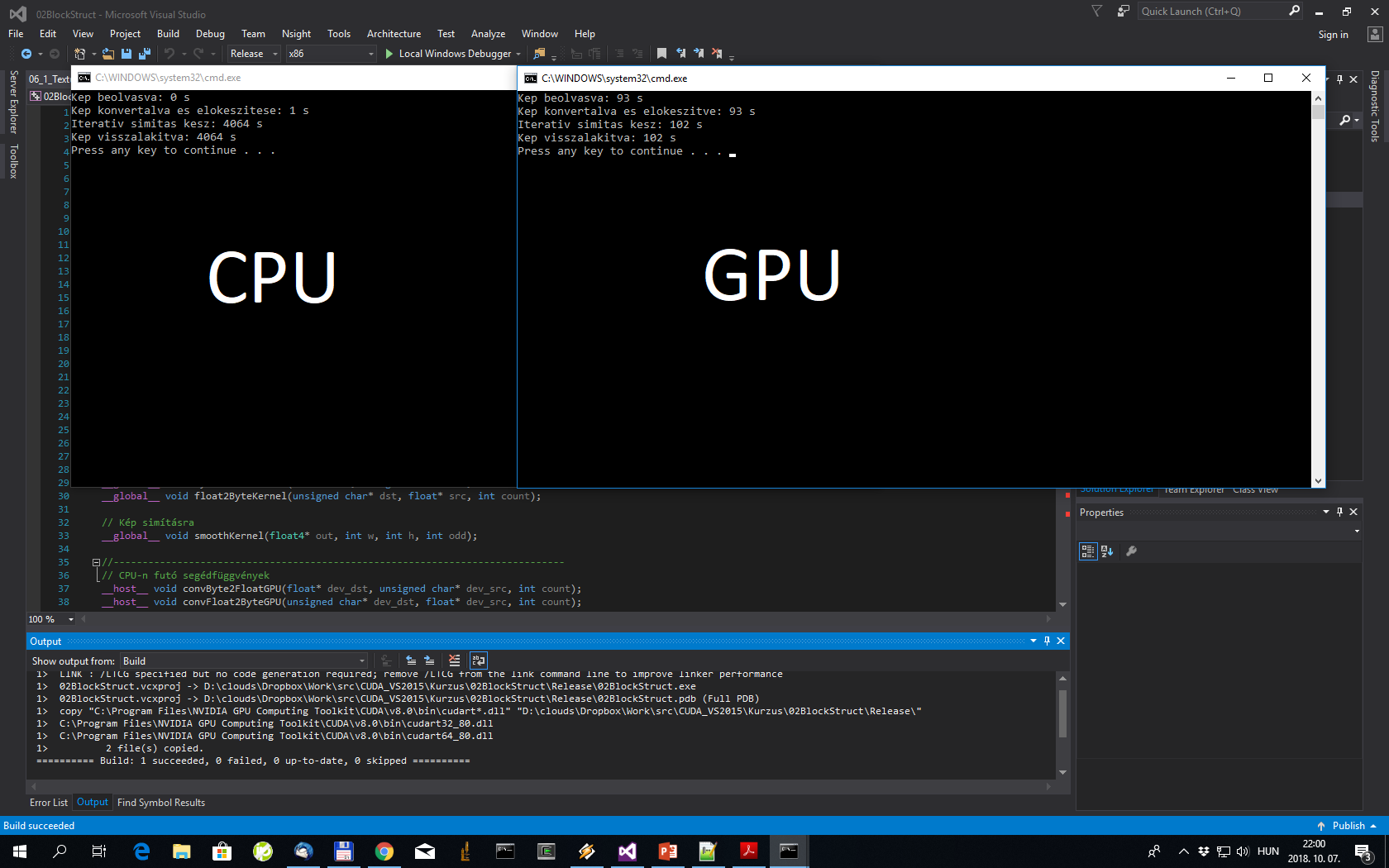
Az egyszerűsödések fő oka, hogy most csak egy-egy példányt kezelünk az adatokból, így nem kell a CPU-GPU közötti adatmozgatással foglalkozni. Egyszerűség továbbá, hogy nem kell kiszámolni az indítási struktúrákat, egyszerűen csak egy-egy for ciklussal bejárjuk a tömböket.

Látni fogjuk viszont, hogy a GPU kód nagyobb komplexitása futási időben megtérülhet.

A simítás képlete a korábbihoz hasonlóan egy külön függvényben történik.

A program ezen része majdnem teljesen megegyezik a kernelekkel. az egyetlen különbség, hogy itt szálanként egy-egy pixelt dolgozunk fel, hanem a számítás köré írni kell egy dupla for ciklust, ami végigiterál a pixeleken.

void smoothOnCPU(float* dst, float* src, int w, int h) {
    int x, y, i, j;

    float temp_r;
    float temp_g;
    float temp_b;
    int counter;

    for(y=0; y<h; y++) {
        for(x=0; x<w; x++) {
            temp_r = 0;
            temp_g = 0;
            temp_b = 0;
            counter = 0;
            for(i=-1; i<2; i++) {
                for(j=-1; j<2; j++) {
                    if(y+i>=0 && y+i=0 && x+j<w) {
                        temp_r += src[4*((y+i)*w + x+j) + 0];
                        temp_g += src[4*((y+i)*w + x+j) + 1];
                        temp_b += src[4*((y+i)*w + x+j) + 2];
                        counter++;
                    }
                }
            }
            dst[4*(y*w+x) + 0] = temp_r / counter;
            dst[4*(y*w+x) + 1] = temp_g / counter;
            dst[4*(y*w+x) + 2] = temp_b / counter;
        }
    }

    return;
}

Láttuk, hogy a konvolúciós simítás CPU kódja sokkal egyszerűbb, és kompaktabb, mint a GPU-n futó változat. A keretprgoramra ez mindenképp szembetűnő, de mintha a kernel is egyszerűbb lenne a CPU-n.

Akkor miért is érdedemes GPU-n futtatnia kódokat? Erre ad választ a lenti kép, ami a program két futásáról mutat statisztikát.

Ha megnézzük a futási időket kiszámíthatjuk az előkészítés, és a számítás vége között eltelt időt, ami maga a számítás ideje. A CPU esetében ez 4063 ezredmásodperc, míg a GPU-nál csak 9 ezredmásodperc. Az gyakorlatilag azt jelenti, hogy a gyorsulás mértéke nagyjából 451-eszeres a GPU javára. Ez jelentheti a különvbséget egy egy másodperces, és egy 7 és fél perces program futási idő között, ami nem elhanyagolható.

A teszteket egy Intel Core-I7-6700 (3.4 GHz) processzor, és egy Tesla K40 GPU használatával mértük.

#include <cstdio>
#include <ctime>
#include <FreeImage.h>
#include <algorithm>

using namespace std;

#define ITERATION_COUNT 100

// ugyanaz a számítás csak a CPU-n.
void smoothOnCPU(float* dst, float* src, int w, int h);

//------------------------------------------------------------------------------
// main
int main()
{
    int i, j;
    unsigned int time;

    unsigned char* image;
    int h, w;

    readRGBImageFromFile("Lena.png", image, w, h);

    time = clock();

    float* temp_src = new float[w * h * 4 * sizeof(float)];
    float* temp_dst = new float[w * h * 4 * sizeof(float)];

    printf("Kep beolvasva: %d s\n", clock()-time);

    for(i=0; i<w*h*4; i++) {
        temp_src[i] = image[i];
    }

    printf("Kep konvertalva es elokeszitese: %d s\n", clock()-time);

    for(i=0; i<1000; i++) {
        if(i%2) {
            smoothOnCPU(temp_src, temp_dst, w, h);
        } else {
            smoothOnCPU(temp_dst, temp_src, w, h);
        }
    }

    printf("Iterativ simitas kesz: %d s\n", clock()-time);

    printf("Kep visszalakitva: %d s\n", clock()-time);

    for(i=0; i<w*h*4; i++) {
        image[i] = temp_src[i];
    }

    writeRGBImageToFile("out.png", image, w, h);

    return 0;
}

void smoothOnCPU(float* dst, float* src, int w, int h) {
    int x, y, i, j;

    float temp_r;
    float temp_g;
    float temp_b;
    int counter;

    for(y=0; y<h; y++) {
        for(x=0; x<w; x++) {
            temp_r = 0;
            temp_g = 0;
            temp_b = 0;
            counter = 0;
            for(i=-1; i<2; i++) {
                for(j=-1; j<2; j++) {
                    if(y+i>=0 && y+i=0 && x+j<w) {
                        temp_r += src[4*((y+i)*w + x+j) + 0];
                        temp_g += src[4*((y+i)*w + x+j) + 1];
                        temp_b += src[4*((y+i)*w + x+j) + 2];
                        counter++;
                    }
                }
            }
            dst[4*(y*w+x) + 0] = temp_r / counter;
            dst[4*(y*w+x) + 1] = temp_g / counter;
            dst[4*(y*w+x) + 2] = temp_b / counter;
        }
    }

    return;
}