Skip navigation

OpenCV DFT

Függvény közelítése szinuszoid függvények összegeként

A DFT 1-dimenziós jelfeldolgozásban is nagyon hasznos.

Az alábbi példa az 1D négyszögjel közelítését mutatja megfelelően kiválasztott szinuszoid hullámok összegeként.

=
+
=
+
=
+
=
+
=

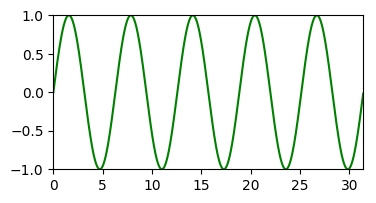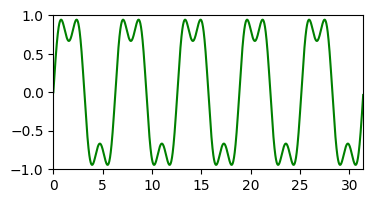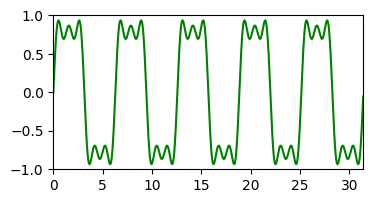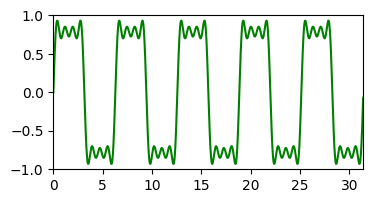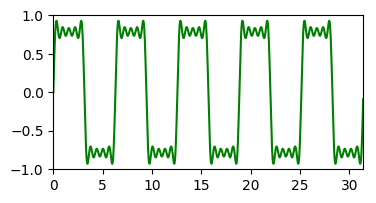Minél több, egyre magasabb frekvenciájú komponenst adunk össze, annál pontosabb négyszögjel közelítést kapunk. A DFT egy bementi jel esetén az abban résztvevő szinuszoid frekvenciák súlyait adja meg. Nem csak négyszögjel, tetszőleges jelsorozat közelíthető megfelelő szinuszoid függvények összegével.

Ez az elv 2D diszkrét raszterképek esetén is használható.

Komplex számokból álló kép kezelése OpenCV-ben

Lebegőpontos típus (CV_32F)

2 csatornából álló kép (valós és képzetes képsík)

Kapcsolódó OpenCV függvények

dft() és idft() Diszkrét Fourier transzformáció és inverze.
getOptimalDFTSize() Mekkorára kell kiegészíteni a kép méretét, hogy működjön a Fourier transzformáció.
copyMakeBorder() Kép megadott méretre kiegészítése.
merge() és split() Egycsatornás képek listájából többcsatornás kép, illetve többcsatornás kép felbontása egycsatornásak listájára, ahogyan korábban is láttuk.
magnitude() Magnitúdó kép számítása valós és képzetes kép alapján.
log() Logaritmus számítása. Specktrum kép megfelelő megjelenítéséhez szükséges, általában log(1 + magnitude(DFT(I))) formában.
normalize() Kép értékkészlet globális átalakítása. A kép megfelelő megjelenítéséhez szükséges.
mulSpectrums() Spektrum képek elemenkénti szorzása. Frekvenciaszűrők alkalmazására használható. A frekvenciaszűrőt külön képként kell előzetesen előállítani.

2D DFT

A 13_02_b_add_periodic_noise_interactive.py példaprogramban láthatjuk, milyen lépések szükségesek egy 2D DFT végrehajtásához.

A példaprogram interaktívan módosíthatóvá teszi a frekvenciakép értékeit.

  • A frekvenciaképen a bal egérgomb lenyomásával az ott található érték képzetes részét jelentősen megnövelhetjük és rögtön láthatjuk az inverz DFT eredményét. Külön ablakban az adott pozícióhoz tartozó 2D szinuszoid hullám képét is láthatjuk. Figyeljük meg, hogy a szimmetrikus konjugált tulajdonság megtartásához az origóra szimmetrikus értéken is elvégezzük a megfelelő módosítást! A bal egérbomb felengedésével az eredeti érték kerül visszaírásra.
  • Ha a bal egérgomb lenyomva tartása mellett mozgatjuk az egeret, folyamatosan láthatjuk a változást.
  • A jobb egérgomb megnyomásával rögzíthetük a megváltoztatott értéket a frakvenciaképben. Ezzel egyre több periódikus zajt adhatunk hozzá a képhez.

Próbáljuk ki a következőket.

  • Mozgassuk az egeret a frekcencia kép közepéhez (origójához). Nyomjuk le a bal egérgombot és nézzük meg a hatását!
  • A bal egérgombot lenyomva tartva mozgassuk az egeret valamilyen irányban a kép széle felé! Megfigyelhetjük, hogy távolodva egyre sűrűbb hullámzást kapunk, valamint a hullámfüggvény iránya merőleges az origóból az egér pozícióba húzott irányra!