Gépi tanulás a gyakorlatban

Túltanulás elkerülése

A torzítás-variancia dilemma

Többször említettük, hogy a felügyelt gépi tanulási feladatnál a célunk, hogy a tanulás során nem látott példákra a lehető legjobb pontásságú predikcióra képes modellt tanuljuk meg, amihez a tanuló algoritmusnak általánosítási készségre van szüksége. Vizsgáljuk meg ezt a kérdést alaposabban!
Hajtsunk végre egy regressziós kísérletsorozatot! Az egyszerűség kedvéért legyen csak egyetlen folytonos jellemzőnk, aminek az értékét az alábbi ábrák x tengelye reprezentál. Vegyök az \( f(x)=2 \sin(1.5x) \) függvényt. Generáljunk 20 egyedet úgy, hogy először egyenletes eloszlásból véletlenszerűen kidobdunk egy \(x\) értéket a 0..5 intervallumon. Majd az \(f(x)\) értékhez hozzáadunk egy véletlenszerűen generált zaj értéket 0 várható értékű normális eloszlásból. Legyen ez a 20 példa a tanító adatbázisunk, ahol a generált \(x\) értékek az egyetlen jellemző értékei és az \(f(x)\)+zaj a célváltozó értéke. Ezzel a módszerrel szimuláljuk a valós életbeli adatbázisokon előforduló zajt. A gyakorlatban a jellemzők és a tanító adatbázis célváltozója is gyakran zajos. Ez a zaj jöhet valamilyen mérési- vagy emberi hibából, de abból is, hogy nem tudjuk pontosan mérni az adott változó értékét és a becslésünk nem pontos.

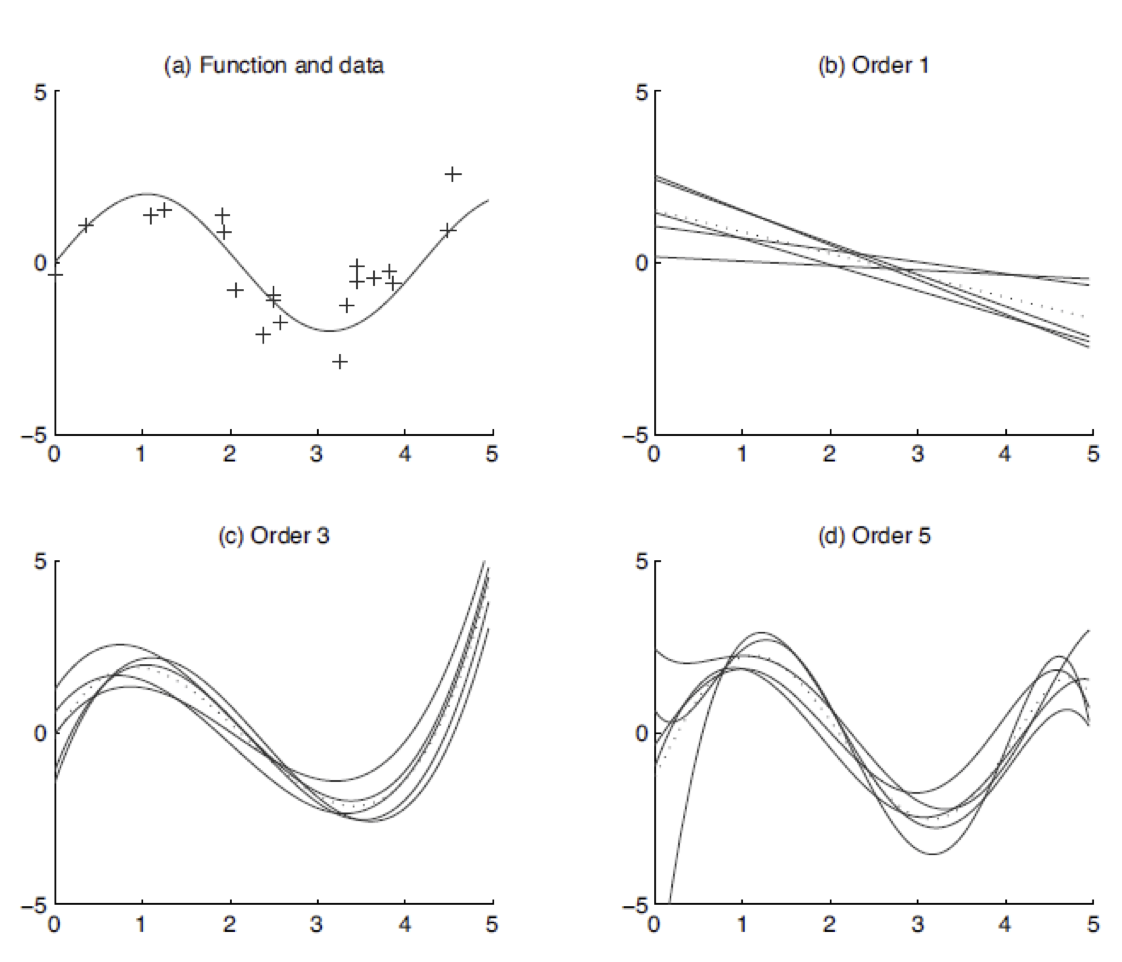
A fenti képen a bal felső ábra vizualizálja a cél \(f(x)\) függvényt és a rendelkezésre álló zajos 20 tanító példát. Ismételjük meg ötször a 20 elemű tanító adatbázis véletlenszerű generálási folyamatát, így lesz 5db, egyenként 20 elemű, tanító adatbázisunk. Az 5 adatbázist ugyanbból az \(f(x)\) függvényből generáltunk, ezért azt várjuk el egy jó gépi tanuló modelltől, hogy az 5 tanító adatbázison tanult 5 modell nem fog nagyon különbözni egymástól, azaz robosztus, tolerálja az zajt.

A fenti kép másik három ábráján 5-5 görbét látunk. Egy ábra 5 görbéje az 5 tanító adatbázison tanított regressziós modellt vizualizálja. A három ábrán három különböző bonyolultságú regressziós modellt tanítunk a tanító példákra, amik első (lineáris), harmad és ötöd rendű polinomokat illesztenek a 20 elemű tanító adatbázisokra. Figyeljük meg, hogy a lineáris modellnél viszonylag nagy lesz a predikciók hibája ha mondjuk az RMSE kiértékelési metrikát használjuk a 20 tanító példán. A modell tanító adatbázison számított hibáját hívjuk torzításnak (bias). A nagy torzítás azt jelenti, hogy a gépi tanulási megközelítés amit választottunk nem tudja jól leírni/megtanulni a tanító adatbázis egyedeit (underfit), egy komplexebb megközelítésre van szükségünk.

Minden 20 ponthoz található olyan ötödfokú polinom, ami szinte tökéletesen illeszkedik a 20 tanító pontra. Viszont az 5db ötödfokú polinom amit 5 különböző adatbázison tanítottunk nagyon eltér egymástól. Ugyanazon eloszlásból vett részmintákon (a gyakorlatban például ha egy tanító adatbázisból véletlenszerűen veszünk több részhalamzt) tanított modellek különbözőségét varianciának (variance) hívjuk. Ha egy gépi tanulási megközelítésnek nagy a varianciája az azt jelenti, hogy túlságosan jól illeszkedik a zajos tanító egyedekre (overfit), túltanul, nem rendelkezik elég általánosítási készséggel, az igazi mögöttes igazi összefüggések (jelen esetben az \(f(x)\) függvény) helyett a zajra épített modellt. Egyszerűbb modellre van szükségünk.

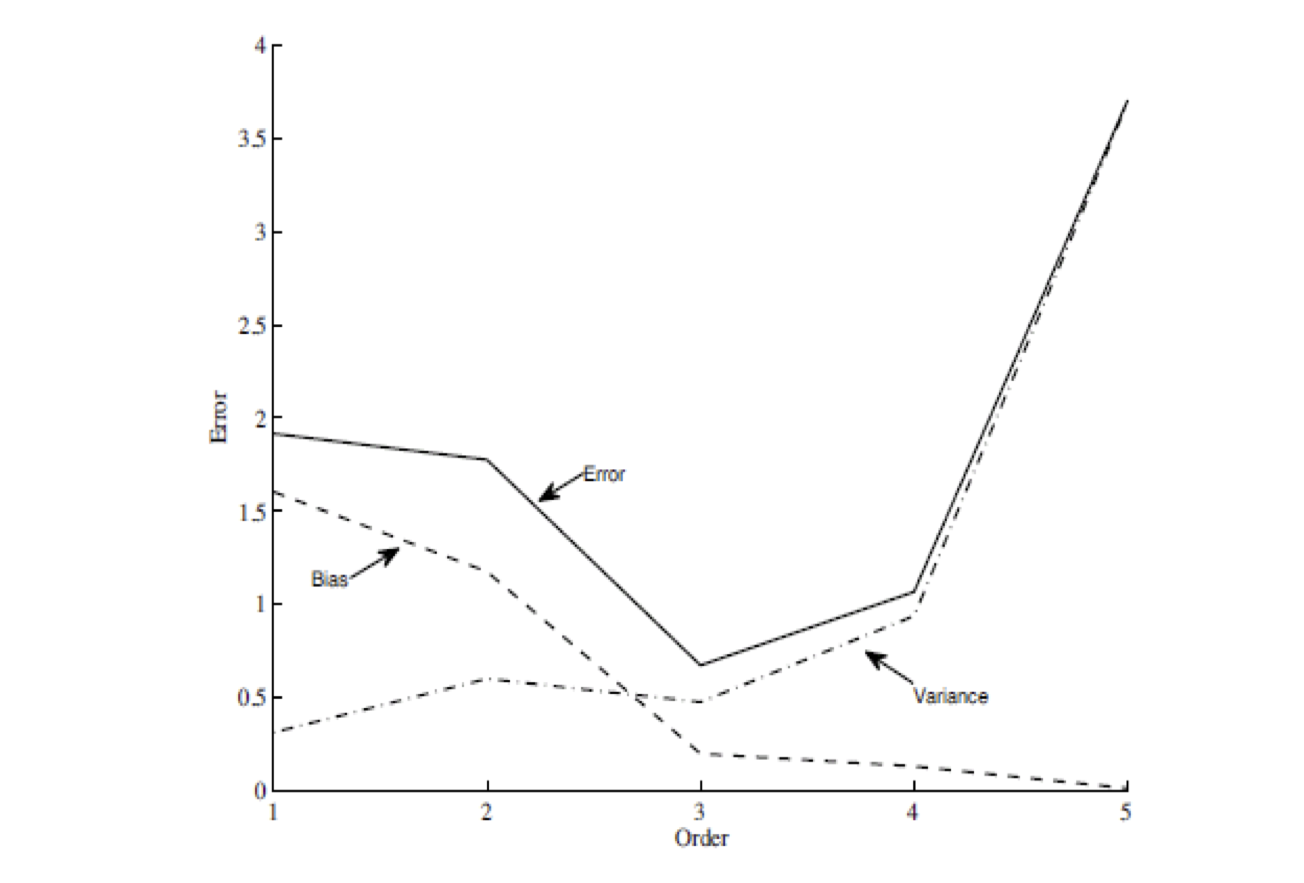
A torzítás és variancia értékeket szemlélteti a következő ábra. Itt a fenti kísérletsorozatot megismetéljük másod és negyedrendű polinomakkal is mérjük a polinomokkal elért torzítást és varianciát. Megmutatható, hogy a modell hibája tanító adatbázisban nem szereplő egyedeken (error) a torzítás és variancia összege.

A torzítás (bias) és variancia számszerűen mérve szimulált adatokon különböző rendű polinomokat használva. Egy felügyel gépi tanulási modell össz hibája (error) a torzítás és variancia összege.Forrás: [Alpydin 2010]

A fenti ábrán jól látszik, hogy a megfelelő komplexitású módszer kiválasztásával érhetjük egy a legkisebb össz hibát. Ezt hívjuk torzítás-variancia dilemmának, ami minden gépi tanulási feladatnál előkerül. Nem csak a túltanulást, de a "túl kevés" tanulást el akarjuk kerülni, azaz minden feladatnál meg kell találnia a mérnöknek azt arany középutat a torzítás és variancia közt, ahol tudunk tanulni valamit a tanító adatbázisból, de a tanult modellnek van általánosítási készsége is, azaz nem tanult túl.

A túltanulás vizuális szemléltetése.Forrás: Udicity

Torzítás-variancia konfigurálása különböző gépi tanulási megközelítéseknél

Meg kell találnunk a konkrét feladathoz, a megfelelő komplexitású modellt. A különböző gépi tanulási módszereknek különböző a komplexitása, az első feladatunk a megfelelő módszer kiválasztása a feladathoz. De szerencsére minden gépi tanuló algoritmus tovább konfigurálható, hogy mennyire torzítson illetve variálódjon. Ez általában egyetlen meta-paraméter, beállításával (mint egy csúszka) érhető el. Ezt torzítás-variancia vagy általánosítás-túltanulás meta-paraméternek hívjuk. Ezt tárgyaljuk az alábbiakban a három korábban megismert gépi tanuló megközelítésnél.

A döntési fa magassága

Egy döntési fa minél nagyobb/mélyebb annál bonyolultabb döntési szabályokat ír le, azaz nagyobb a komplexitása, annál nagyobb a veszélye a túltanulásnak (túl nagy varianciának). A különböző döntési fa implementációkban különböző módokon tudjuk szabályozni, hogy milyen mély fát engedünk építeni a tanulás folyamán. Van ahol explicit korlátozhatjuk a tanult fa mélységét, de van ahol azt adhatjuk meg, hogy a tanító adatbázisban legalább hány egyed eshet egy döntési szabállyal szűrt halmazba. Ha egy döntési levél mindössze kevés tanító adatbázisbeli elemre érvényesül akkor nagy a veszélye, hogy csak zajt tanulunk és nem a modellezni kívánt igazi szabályokat/összefüggéseket.

Vegyük elő a korábbi döntési fát a tenisz osztályozási feladathoz. Mi történne ha egyetlen új tanító példa érkezne Égbolt=Napos, Hőmérséklet=Forró, Páratartam=Magas, Szél=Erős jellemzővektorral és Tenisz=Nem osztálycímkével. Hogy erre az egyedre is helyes döntést hozzon a döntési fa ki kell egészítenünk a fát és a Páratartalom=Normál levél helyett egy belső csúcsot felvenni, ami képes a különböző címkéjű Égbolt=Napos és Páratartam=Magas egyedeket elkülöníteni egymástól. Egyetlen (lehet, hogy zajos) példa alapján építettük a fát...

A lineáris gépek regularizációja

Az Occam borotvája elv alapján, ha egy fogalmat különböző modellekkel is ugyanolyan pontosan le tudunk írni, akkor a modellek közül válasszuk a legegyszerűbbet! A legkevésbé specifikus/komplex modelltől azt várhatjuk ugyanis, hogy jobb az általánosítási készsége, azaz a korábban nem látott példákra nagyobb valószínűséggel fog pontosabb predikciót adni.

*Occam borotvája.* Forrás: clubstreetpost.com

A lineáris gépeknél pontosan az Occam borotva elvét követik. Ott a modell mindig egy fix hosszúságú \(w\) súlyvektor. Egy súlyvektor annál "egyszerűbb", minél kisebb a hossza. A lineáris gépek tanítása egy optimalizációs feladat, ahol keressük azt a modellt/súlyvektort ami minimalizálja a tanító adatbázisokon mért hibát (például RMSE). A gyakorlatban ezt a célfüggvényt kiegészítjük és a hiba minimalizálása mellett a legegyszerűbb modell elérésére is bevezetünk egy ún. regularizációs tagot. Egy regularizációs konstanssal a mérnök konfigurálja, hogy a célfüggvénybe a regularizációs tag mennyire hangsúlyos a hiba minimalizációs taggal szemben. Továbbá kiválaszthatja a regularizáció formáját (hogyan mérjük a súlyvektor hosszát). A leggyakoribb súlyvektor regularizációs forma az L1 és L2 normák.

k szerepe a kNN osztályozóban

A k legközelbbi szomszéd osztályozónál maga a k értéke játsza a torzítás-variancia szabályozó meta-paraméter szerepét. Gondoljuk végig k szélsőséges értékei esetén mi történik! k=1 esetén csak egyetlen legközelebbi szomszéd alapján dönt, ami lehet, hogy csak zaj. Itt óriási a variancia, túltanulunk. Ha k a tanító adatbázis mérete, akkor pedig minden ismeretlen egyedre ugyanaz lesz a predikció, hiszen mindig minden tanító adatbázisbeli a szomszédságba esik, és a predikció a teljes tanító adatbázis leggyakoribb osztálycímkéje lesz (pont ugyanaz, mint a most frequent class baseline megoldásé).

Meta-paraméterek finomhangolása a gyakorlatban

Egy kiválaszott gépi tanulási módszer torzítás-variancia meta-paraméterét egy konkrét adatbázison csak úgy tudjuk beállítani/finomhangolni, kipróbálunk különböző értékeket és ezek alapján kiválasztjuk a legjobbnak vélt meta-paraméter értéket. Mivel több meta-paraméter értéket kell 'tanulás majd kiértékelés' formájában tesztelnünk ezért ezt nem csinálhatjuk a korábban kialakított tanító/kiértékelő adatbázis vágás végrehajtásával. A meta-paraméter finomhangolás ugyanis a gépi tanulás része, ha a kiértékelő adatbázison legjobban teljesítő meta-paramétert használnánk a végső modellhez, akkor ott már valamennyi információt szereztünk a kiértékelő adatbázisról, azaz nem szimuláljuk, hogy a modellt a tanítás során nem látott példákon értékeljük ki! Ezt az információszivárgást a kiértékelő adatbázisról hívjuk kukucskálásnak (peeking). Ezért a helyes módszertan az, hogy a rendelkezésre álló címkézett adatbázist három részre vágjuk: tanító (training), validációs (validation vagy development) és kiértékelő/teszt (evaluation vagy test) részhalmazokra. A kiértékelő adatbázist félre tesszük, és egyetlen egyszer a végső modell kiértékelésére használjuk csak. A különböző meta-paraméterek pontosságának kiértékelésére a tanító adatbázison tanítunk és a validációs halmazon értékeljük ki. Felhívom a figyelmet, hogy a gépi tanulási rendszer minden változtatását (például új jellemző felvételének hatását) a validációs halmazon helyes kimérni.

A meta-paraméter finomhangoláshoz, érdemes egy konkrét meta-paraméter érték mellett tanított modellt a vaildációs halmaz mellett a tanító adatbázison is kiértékelni. Az alábbi ábra szemlélteti, hogy hol van az ideális értéktartomány a meta-paraméternek. Túltanulásnál a tanító adatbázison mért hiba tovább csökken, de az ismeretlen példákon mért hiba nő. Ez már nem jó. Az arany középutat kell megtalálnunk.

Az x tengelyen egy algoritmus torzítás-variancia meta-paraméterét látjuk és annak hatását a tanító adatbázison (piros) illetve validációs halmazon (zöld) mért hibára. A tanuló algoritmus komplexitást úgy kell beállítani, hogy a hiba a lehető legkisebb legyen a validációs halmazon.