Felügyelet nélküli gépi tanulás

A kurzuson eddig felügyelt gépi tanulással foglalkztunk. Ebben a leckében a gépi tanulás egy másik részterületével, a felügyelet nélküli tanulással ismerkedünk meg. A felügyelet nélküli tanulás olyan gépi tanulási feladat ahol a cél jelöletlen/címkézetlen adat leírása rejtett struktúrák/összefüggések feltárásával.. Sok féle rejtett struktúrát akarhatunk feltárni, de a leggyakoribb alkalmazások:

  • A klaszterezés (clustering) egy adatbázis címkézetlen egyedeinek olyan csoportjainak megtalálása felügyelet nélküli tanulási keretben, hogy az egy csoportban levő egyedek hasonlóbbak lesznek egymáshoz, mint a más csoportban levőkhöz. Ilyen alkalmazás lehet például ügyfelek klasztereinek (csoportjainak) azonosítása múlt beli tranzakcióik alapján, vagy egy ajánló rendszerben filmek csoportosítása aszerint, hogy milyen felhasználóknak tetszettek.
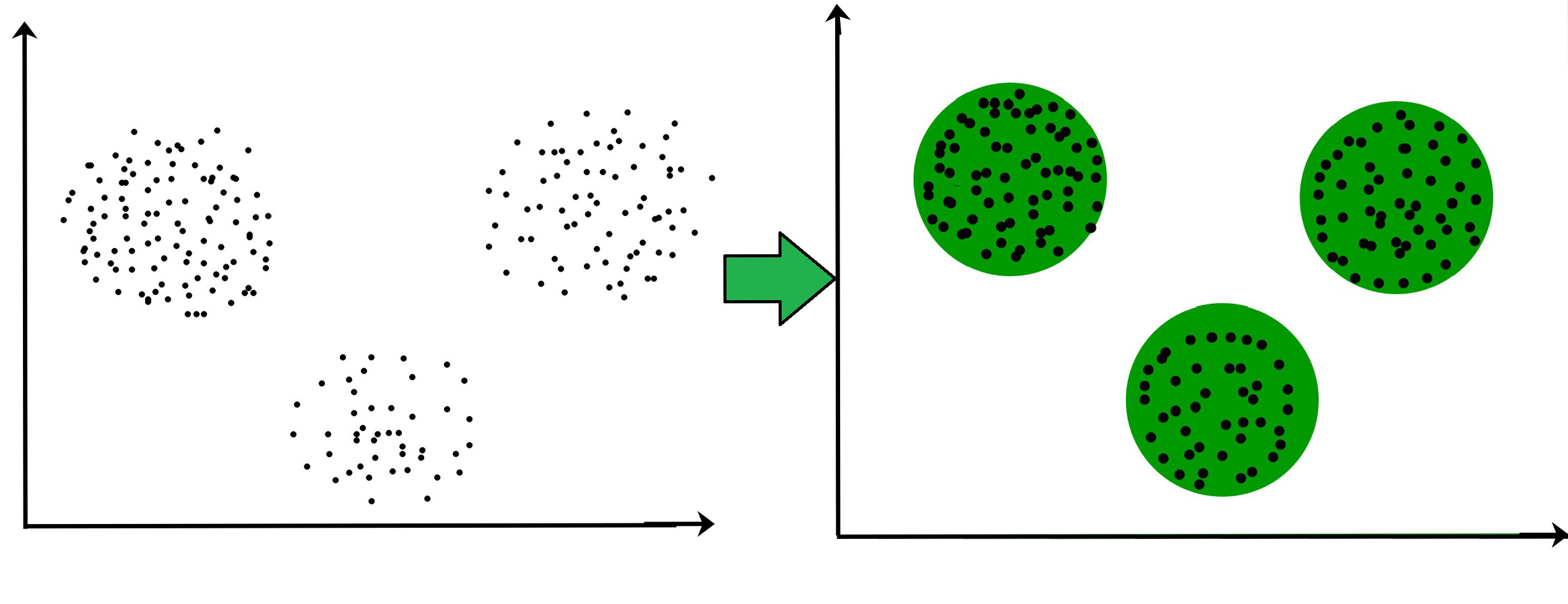
    A klaszterzési feladatban címkézetlen egyedek csoportosulását tárjuk fel.Forrás: geeksforgeeks.org
  • A dimenzió csökkentés (dimensionalty reduction) célja, hogy egy adatbázis egyedeinek jellemzőterére adjon egy olyan transzformációt amiben az egyedek egy jóval kisebb dimenziószámú térben írhatóak le, de az eredeti jellemzőtér tulajdonságai minél kevésbé torzuljanak. Például egyes dimenzió csökkentő eljárások azt tűzik ki célul, hogy az eredei jellemzővektorok közti páronkénti hasonló metrikához közeli hasonlósági értékeket kapjuk az egyedek páronkénti összehasonlításakor az új, kisebb dimenziós térben. A gyakorlatban a dimenzió csökkentést arra használjuk általában, hogy 2D vagy 3D ábrán tudjuk vizualizálni egy adatbázis, eredetileg sokezer jellemzővel leírt egyedeit.
    Egy ajánló rendszer esetén a filmek és felhasználók nagy dimenziós jellemzőtérrel vannak leírva. Dimenzió csökkentési eljárásokkal ezeket a jellemzővektorokat 2 dimenzóssá transzformálhatjuk és megjeleníthetjök egy koordináta rendszerben. Ha két film közelebb van egymáshoz akkor hasonlóak (valamilyen értelemben) illetve ha egy felhasználó közel van egy filmhez az azt jelenti, hogy azt preferálja.
A felügyelelet nélküli tanulás is gépi tanulás, hiszen van egy jól definált feladat (pl. klaszterezés) és azt várjuk el, hogy a rejtett struktúrákat pontosabban tárják fel az algoritmusok (azaz teljesítményük javul) ha több adatunk van. Itt is egyedekkel és azokat leíró jellemzővektorokkal dolgozunk. Azonban a fenti néhány alkalmazási példából látszik, hogy a felügyelet nélküli gépi tanulás elsősorban az adatmegértésben segíti a mérnök munkáját. Esetleg a feltárt rejtett összefüggéseket (klaszterek, csökkentett dimenzótér) be lehet építeni nagyobb rendszerekbe - például egy felügyelt gépi tanulási megoldásba jellemzőként -, de itt nincsen szó döntésről/predikcióról, általánosítási készségről.
Számtalan klaszterező ill. dimenzió csökkentő algoritmus létezik. Az alábbiakban egy-egy algoritmust mutatunk be röviden.

k-közép: egy klaszterező algoritmus

A k-közép (k-means) algoritmus célja egy adatbázis egyedeinek partícionáló klaszterezése, azaz k darab csoport/klaszter lesz a kimenet, ahol az adatbázis minden egyede pontosan egy klaszterbe tartozik. A mérnöknek előre meg kell adni k értékét (azaz hány klasztert szeretne látni) és az egyedek közti páronkénti hasonlósági metrikát.
A k-közép algoritmus k darab klaszter középpontot (centroid) frissít egy iteratív algoritmus során. Alapgondolata, hogy egy klaszterben levő pontok közelebb vannak saját klaszterük középpontjához, mint bármely más klaszter középpontjához.

Az egyes pontok két dimenziós jellemzőtérrel leírt ímkézetlen egyedek. A k=3 k-közép algoritmus 3 centroidot (keresztek) tart nyilván, az ábrán, a tanulás végén minden egyedet kiszíneztünk a klaszterbe tartozás szerint.

SVD mint dimenzió csökkentő algoritmus

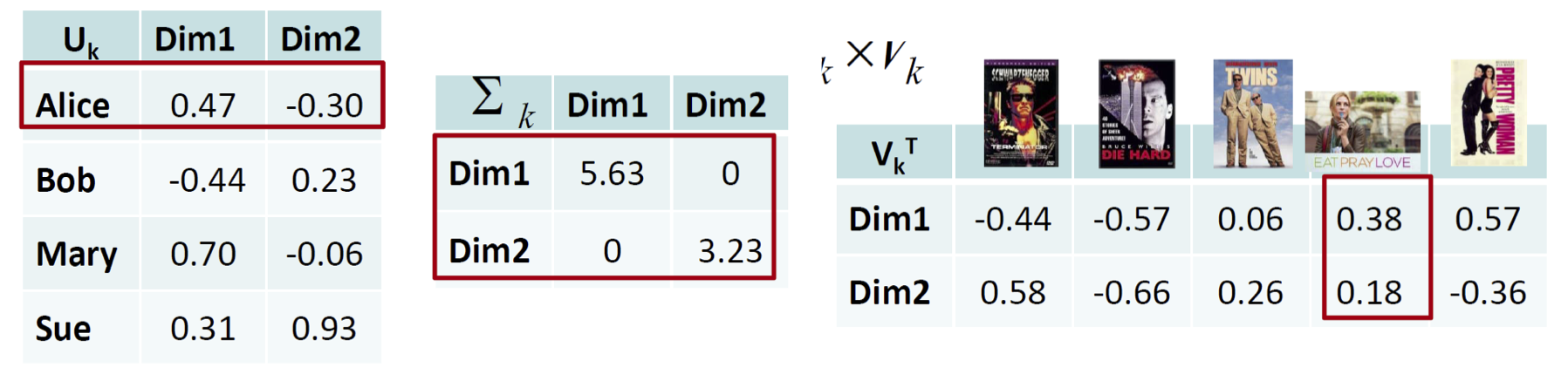
Az egyedeinket leíró jellemzővektorok egy mátrixot alkotnak. Egy mátrix szinguláris érték felbontása (singular value decomposition) három mátrix szórzataként írja fel az eredeti mátrixot: jobb sajátvektorok mátrixa, sajátértékek diagonális mátrixa és bal sajátvektorok. Minden egyedhez egy bal sajátvektor, minden jellemzőhöz egy jobb sajátvektor tartozik. A legnagyobb sajátértékekhez tartozó sajátvektorok járulnak hozzá a legjobban az eredi mátrix magyarázatához. Ha csak néhány legnagyobb sajátértékhez tartozó vektort számolunk ki - a többit kihagyjuk/levágjuk (truncate) - akkor egy közelítését kapjuk az eredeti mátrix felbontásának. Viszont a néhány sajátvektor, amit megtartunk jól közelíti az egyedek jellemzővektorainak és a jellemzők értékvektorainak tulajdonságait, ezért használhatjuk őket, mint csökkentett dimenziójú vektortér. Ráadásul az egyedek és jellemzők ugyanabban a kis dimenziós térben kerülnek reprezentálásra.

Ha felhasználók az egyedeink és egyes filmekre adott értékelésük a jellemzőtér akkor az SVD felbontás három mátrix szorzatára bontja az egyed-jellemző mátrixot. Ha csak a két legnagyobb sajátértékhez tartozó vektorokat számoljuk ki (Dim1 és Dim2) akkor ezek segítségével a a felhasználókat és a jellemzőket megjeleníthetjük egy 2D koordinátarendszerben.

Felügyelet nélküli gépi tanulás a gyakorlatban

A felügyelet nélküli gépi tanulási feladatnál a mérnöknek nagyon pontosan kell definiálni a feladatot. Nem csak a megfelelő hasonlósági függvény definálása (a hasonlósági függvény fontosságát korábban tárgyaltuk) tartozik itt a feladat definíciójába. Például ha a k-közép algoritmus választjuk a számtalan klaszterező algoritmus közül akkor azt is megadjuk, hogy "klaszter-középpont-alapú" kalaszterezési feladatot akarunk megoldani. Számtalan klaszterezési megközelítés létezik (pl. hierarhikus vagy sűrűség-alapú), amik mind más típusú klaszterezési feladatot oldanak meg, más a céljuk.

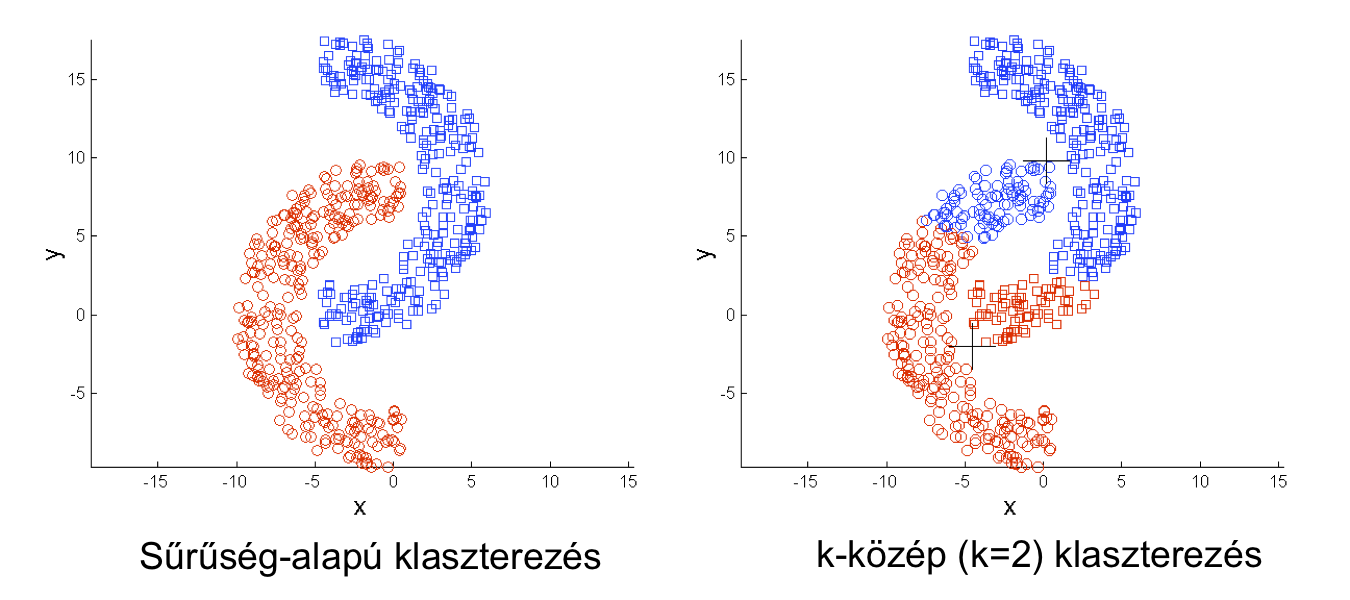
Ezen a két dimenziós adathalmazon a bal oldalon a "sürűség-alapú klaszterezési" feladat, jobb oldalon a "klaszter-középpont-alapú kalaszterezési feladat" megoldásait látjuk színezéssel. A két feladatnak más a célja!

Mivel a felügyelet nélküli gépi tanuló címkézetlen adattal dolgozik (azaz nincs felügyelet), ezért nem lehet explicite kiértékelni egy lehetséges megoldást. Például a felügyelt tanulásnál lefuttattuk a tanulót különböző meta-paraméter értékekkel és meg tudtuk mondani melyik paraméter érték teljesítménye jobb. K-közép klaszterezőnél nem tudjuk kiértékelni/mérni, hogy két k érték közül melyik teljesít jobban!

A bal felső ábrán látszanak a 2D címkézetlen egyedek. Ezen az adatbázison hány klaszter van? A k-közép algoritmus milyen k esetén teljesít a legjobban? Nem lehet összehasonlítani vagy objektíven kiértékelni! A szemlélő szubjektív megítélésétől függ.
Vannak klaszter-validációs metrikák amik számszerűsítenek bizonyos tulajdonságait egy klaszterezési megoldásnak (például SSE vagy klaszter kohézió). Ezek segíthetnek a mérnöknek megérteni egy klaszterezési megoldást, de nem mutatják meg a klaszterezés jóságát/pontosságát, hiszen az, hogy mennyire jók az eredményül kapott klaszterek a szemlélőtől (mérnök) is függenek! Ezért nem szabad összekeverni a klaszter-validációs metrikákat a felügyelt tanulás kiértékelési metrikáival!

Ellenörző kérdések

  1. Ha adott ügyfelek csoportosítása (a marketing osztály által definiált tipikus váráslói szokásokkal íbó minta ügyfelek) akkor ez felügyelt vagy felügyelet nélküli gépi tanulási feladat?
  2. Miért használunk dimenzió csökkentő algoritmusokat?
  3. Hogyan értékeljük ki a felügyelet nélküli tanuló módszereket?

További ajánlott irodalom

  • A k-közép mellett a hierarhikus, gráf-alapú és sűrűség-alapú klaszterezést is elmagyarázom ebben a diasorban.
  • Az SVD matematikai alapjait ismerteti az SzTE "KÖSZI haladóknak" kurzusa.
  • Kitekintés: az SVD mellett számos dimenzió csökkentő megközelítés létezik. Ezek közül a legfontosabbakat jól bemutatja ez a blog poszt