Lokális osztályozók

Ha az osztályozási feladat olyan, hogy kézenfekvő módon tudunk az egyedek közt hasonlósági (vagy távolság) függvényt megadni, akkor a legegyszerűbb osztályozási megközelítést érdemes alkalmaznunk, az ún. k legközelebbi szomszéd (k nearest neighbour, kNN) osztályozót. Tehát tegyük fel, hogy adott egy osztályozási feladat és egy címkézett tanító adatbázis valamint egy függvény, ami számszerűsíti bármely két egyed távolságát. Ekkor, a k legközelebbi szomszéd osztályozó algoritmus úgy predikál, hogy

  1. megkeresi a tanító adatbázisban azt a k darab egyedet amelyek a leghasonlóbbak a predikálandó egyedhez (a hasonlósági függvény maximuma/távolság függvény minimuma a kérdéses egyed és a tanító példa közt). Ezek lesznek a legközelebbi szomszédok.
  2. Majd a k legközelbbi szomszéd osztálycímkéiből kiválasztja a leggyakoribbat és azt predikálja.
Legyen két folytonos jellemzőnk \(x_1\) és \(x_2\). Az alábbi ábrán a színes pontok a tanító adatbázis egyedei, amiknek két koordinátája a két jellemző, színük pedig az osztálycímkét jelöli. Legyen az egyedek közti távolság mérték az euklideszi távolság. Középen az x pont egy egyed amire predikálni szeretnénk. A k=5 legközelebbi szomszéd (euklideszi távolság alapján) a körön belüli 5 tanító adatbázisbeli egyed. Az öt szomszédból kettő piros és három fekete, ezért a fekete osztályt fogja predikálni az osztályozó.
kNN osztályozó (k=5) működése két jellemző alapján megfogalmazott euklideszi távolság függvény alapján.Forrás: [Duda 2000]
Bináris osztályozás esetén érdemes páratlan k-t választani, hogy a holtversenyeket elkerüljük. Holtversenyek feloldására egyébként súlyozhatjuk a címkéket a kérdéses egyedtől mért távolsággal.
A kNN a lineáris gépekhez hasonlóan folytonos jellemzőterek esetén használatos. Míg azonban a lineáris gépek egy olyan osztályokat elválasztó döntési felület keresnek ami globálisan, az egész jellemzőteret átszeli, a kNN a jellemzőtérben lokális információk alapján dönt, hiszen a szomszédságon/lokális környezetn kíül eső tanító adatbázisbeli egyedek egyáltalán nem játszanak szerepet az osztályozási döntésben.
A k legközelebbi szomszéd osztályozó egy érdekessége, hogy nincs modellje. Minden egyes predikciónál ki kell számolni a páronkénti távolságot a kérdéses egyed és az összes tanító adatbázisbeli elem között, hogy a legközelebbi szomszédokat megtaláljuk. Nincs modell, de a gépi tanulás szükséges feltételét, miszerint egyre nagyobb tanító adatbázisból egyre jobb osztályozási pontosságot érjünk el, teljesíti.

kNN a gyakorlatban

A k legközelebbi szomszéd osztályozó teljesítménye azon áll vagy bukik, hogy milyen távolság/hasonlóság függvényt definiálunk. A gyakorlatban sajnos ezzel nem nagyon törődnek a mérnökök. Ha az egyedek le vannak úgyis írva egy jellemzőkészlettel akkor egyszerűen a két jellemzővektor valamilyen standard vektortávolságát (koszinusz vagy euklideszi távolság) szokták használni. Ez nagyon veszélyes!
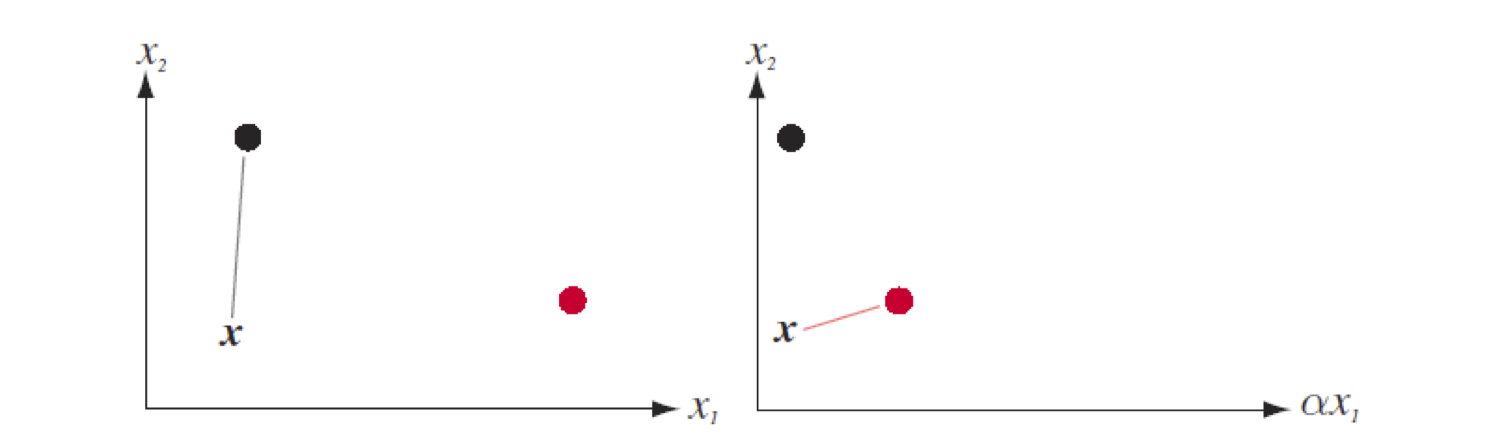
Legyen megint két jellemzőnk \(x_1\) és \(x_2\), valamint két osztályunk piros és fekete. Továbbra is használjuk a 2 dimenziós euklideszi távolságot. A tanító adatbázisunk csak egy-egy példából áll az alábbi ábrákon. A bal oldali ábrán a predikálandó x ponthoz a fekete tanító példa van közelebb, így a k=1 legközelebbi szomszéd osztályozó feketét predikál. Szorozzuk meg minden egyed \(x_1\) értékét egy \(\alpha\) konstanssal (például eddig cm-ben volt megadva egy méret, amit innentől dm-ben szeretnénk tárolni \(\alpha\)=0.1). Ekkor már a piros tanító példa lesz közelebb a kérdéses x egyedhez és azt fogja a k=1 legközelebbi szomszéd osztályozó feketét predikálni! Pedig az egyedeink nem változtak semmit...

kNN osztályozó (k=1) mást fog predikálni ha minden egyed \(x_1\) értékét megszorozzuk egy \(\alpha\) konstanssal.Forrás: [Duda 2000]
Az euklideszi (és minden egyéb általános vektorhasonlósági) távolsággal vigyázzunk tehát mert ha vannak olyan jellemzők amiknek az értékkészlete nagy akkor elnyomják azokat amiknek kicsi. Ennek kivédésére érdemes a folytonos jellemzőinket normalizálni, azaz egy értékkészletre hozni. De ez nem oldja meg minden problémánkat, az általános vektorhasonlóságok informálatlanok, azaz nem képesek a jellemzők döntésben játszott szerepét megtanulni (szemben a döntési fákkal vagy lineáris gépekkel).

kNN előnyei:

  • Jó távolság metrika esetén nagyon jó eredményt tud elérni.
  • Ha a folytonos jellemzőtérben nem lineárisan elválaszthatóak az osztályok, a kNN akkor is jó eredményt tud elérni.

    • kNN hátrányai:

    • Jó távolság függvény mérnöki megadása nagyon nehéz.
    • Ha a tanító adatbázis nagyon nagy, lassú lehet a predikció. (Ennek orvoslására számtalan térindexelésen alapuló megoldás létezik, lásd k-d tree.)
    A k legközelebbi szomszéd osztályozót tehát akkor érdemes választani ha természetesen módon adott egy egyed párok hasonlóságát/távolságát leíró metrika vagy a folytonos térben nagyon bonyolult az osztályokat elválasztó döntési felület, azaz nem bízunk a globális modellben, hanem a tér lokális tulajdonságaira építjük modelljeinket.

    Ellenörző kérdések

    1. Képek esetén milyen hasonlóság függvényt használnál?
    2. Szózsák modellel adott szöveges dokumentumok esetén, érdemes használni a kNN-t?

    További ajánlott irodalom

    • Különböző, gépi tanulásban használatos vektorhasonlósági metrikák egyszerű bemutatása olvasható itt.