• Introduction
• Project
• Solutions
• The Team
• Download

Introduction

The aim of tomography is to get image of object sections. This method is mostly used in medicine, but also in other fields like archeology, biology, geophysics, materials science, industrial inspection, etc.

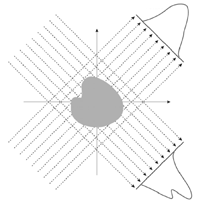
In medical tomography the section images are obtained by moving an X-Ray beam around the object (patient) and record the projection on a film positioned diametrically opposed to the X-Ray beam.

Modern tomography techniques base on collecting projection images from multiple angles and feed them to a tomography reconstruction software algorithm to obtain the section image.

The object, from the mathematically point of view, corresponds to an attenuation function, for which some integrals or sums over a subset are known. Thus two types of tomography reconstruction are posed: continuous tomography and discrete tomography. The continuous tomography assumes that both the domain and the range of the function (object) are continuous.

Binary tomography is one special case of discrete tomography, where the function (object) can take only 2 values: 0 or 1.

So, practically, the aim of binary tomography is to reconstruct a binary image, where the object is represented in white and the background in black, using projections of the image from few different angles.

On the other hand, in discrete tomography, the domain of the function could be either continuous or discrete, but the range of the function is a finite set of real numbers.

Usually, in discrete tomography only a few projections are used, thus the algorithms developed for continuous tomography fail in this case. This method is used because the object needed to be reconstructed has fewer levels of intensity and the number of projections could be reduced.

Common algorithms

Here is a list of common algorithms used in discrete tomography: