Tégla 01 feladat

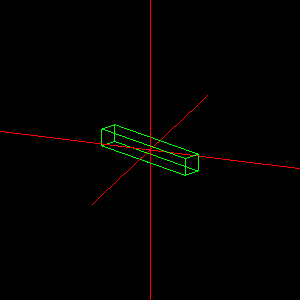
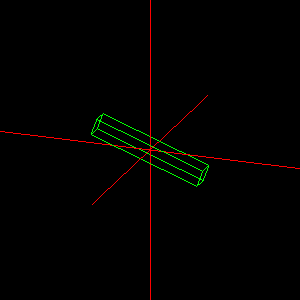
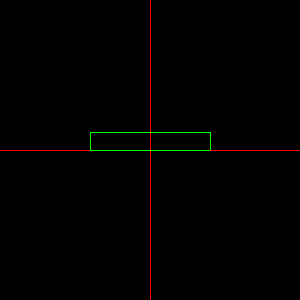
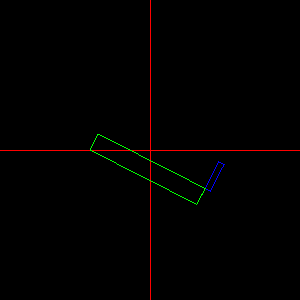
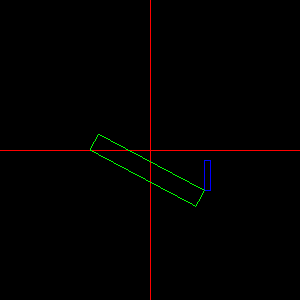
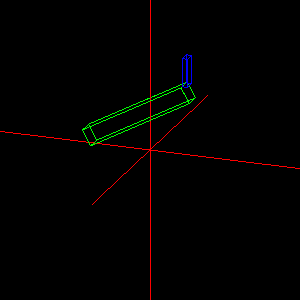
Feladat: Modellezzünk origó középpontú téglatestet, amit az Y-tengely körül a [-30,30] fok tartományban folyamatosan oda-vissza forgatunk.

Megoldás: A rot1 változó tartalmazza az aktuális elforgatási szöget, amit időzítő segítségével változtatunk. Téglatestet kockából nyerünk, skálázás alkalmazásával.

  glPushMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glRotatef( rot1, 0.0, 1.0, 0.0 );
  glScalef( 20.0, 3.0, 3.0 );

  glutSolidCube( 1.0 );

  glPopMatrix();

 tegla01.c

Tégla 02 feladat

Feladat: Mint az előző, csak most a Z-tengely körül forgassunk.

  glPushMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glRotatef( rot1, 0.0, 0.0, 1.0 );
  glScalef( 20.0, 3.0, 3.0 );

  glutSolidCube( 1.0 );

  glPopMatrix(); 

 tegla02.c

Tégla 03 feladat

Feladat: A második példához hasonlóan most is a Z-tengely körül forgassunk, viszont a téglatest alsó lapja helyezkedjen el alapból az Y=0 síkon.

Kérdés: Hogyan változnak az eltolás paraméterei, ha a függvényhívást a skálázás és a forgatás elé írnánk?

  glPushMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glRotatef( rot1, 0.0, 0.0, 1.0 );
  glScalef( 20.0, 3.0, 3.0 );
  glTranslatef( 0.0, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix();

 tegla03.c

Tégla 04 feladat

Feladat: Az előzőkön túl a téglatest "bal alsó", Z-tengely irányú éle haladjon át az origón.

  glPushMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glRotatef( rot1, 0.0, 0.0, 1.0 );
  glScalef( 20.0, 3.0, 3.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix(); 

 tegla04.c

Tégla 05 feladat

Feladat: Az elforgatás után a téglatest éle kerüljön vissza az eredeti helyére.

  glPushMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glTranslatef( -10.0, 0.0, 0.0 );
  glRotatef( rot1, 0.0, 0.0, 1.0 );
  glScalef( 20.0, 3.0, 3.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix(); 

 tegla05.c

Tégla 06 feladat

Feladat: A téglatest jobb felső éléhez modellezzünk egy kék színű kisebb téglatestet, ami követi a mozgást.

  glPushMatrix();

  glTranslatef( -10.0, 0.0, 0.0 );
  glRotatef( rot1, 0.0, 0.0, 1.0 );

  glColor3f(0.0, 0.0, 1.0); 
  glPushMatrix();

  glTranslatef( 20.0, 3.0, 0.0 );
  glScalef( 1.0, 5.0, 2.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glScalef( 20.0, 3.0, 3.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix();

 tegla06.c

Tégla 07 feladat

Feladat: Biztosítsuk, hogy a kék téglatest mindig függőleges maradjon.

  glPushMatrix();

  glTranslatef( -10.0, 0.0, 0.0 );
  glRotatef( rot1, 0.0, 0.0, 1.0 );

  glColor3f(0.0, 0.0, 1.0); 
  glPushMatrix();
  glTranslatef( 20.0, 3.0, 0.0 );
  glRotatef( -rot1, 0.0, 0.0, 1.0 );
  glScalef( 1.0, 5.0, 2.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );
  glPopMatrix();

  glColor3f(0.0, 1.0, 0.0); 

  glScalef( 20.0, 3.0, 3.0 );
  glTranslatef( 0.5, 0.5, 0.0 );

  glutSolidCube( 1.0 );

  glPopMatrix();

 tegla07.c

Tégla 08 feladat

Feladat: A testek mozgása ne egyenletes, hanem gyorsuló-lassuló legyen.

Ötlet: Számítsuk ki előre egy táblázatba a szinusz szögfüggvény értékeit [0,PI/2] között megadott lépésközzel. A rot1idx változó adja az aktuális szinusz érték indexét, amivel a maximális kitérés értékét megszorozzuk. Így kapjuk meg rot1 értékét.

 tegla08.c

Tégla 09 feladat

Feladat: A testek változó sebességű, pattogó mozgást végezzenek.

Ötlet: Mint az előző feladatnál, csak itt a rot1idx változó értéke csak pozitív lehessen.

 tegla09.c