
Group E:
Richárd Jónás (Hungary), Johann Kim (Austria),
Juha Kivijärvi (Finland), Joakim Lindblad (Sweden) &
Beata Szurgot (Poland)
1. The problem
Project 3:
Block world line drawing generated from range image input of scene.
Input: 2D Image of 3D block world as a range image where pixel value
is a function of distance (or simulation) from digital/video camera.
Suggestion, generate synthetic data first, then try out on real data.
Operation: Identification of lines and corners, linking of this to extract
model of scene.
Output: Line drawing of scene. Rotation of object to create new scene.
2. Possible approaches on detecting boxes
There are different ways the boxes could be detected. One could try
to recognize the corners of the boxes. In the noiseless situation the
closest corner would be simple - it would be the closest point in the
image. One could try to find the other corners with some heuristic,
too, and build boxes out of them. The hidden corners and edges would
seem to be a problem with this kind of solution. It also would seem
to badly suffer from noise.
One could also try to find the edges by an edge detection algorithm and
reconstruct the boxes from these. Also this seems to be easily affected
by noise.
The third approach would be to recognize planes.
One way to do this is to compute gradients at every point. The areas
of similar gradients would be the faces of the boxes.
However, the gradient method is very easily disturbed by noise.
The method we selected was to find planes using a 3D Hough transform
and construct the boxes from these. This seems to be the most robust
selection as more points can be used and thus we have more data for
approximation.
3. Our solution
Our solution for the problem is to find planes from the image. This
is done by a 3D Hough transform. The strongest triplets of orthogonal
planes are found and the boxes are constructed from these. This method
is very robust as noise does not make a great change to the result of
the 3D Hough transform. The algorithm works in the following way:
a. Background removal
In the first step the background is detected and set to infinity. This
is done by simple thresholding. This step is not necessary for the
artificially created images as the background can be set to infinity in
the creation process. The background detection is not crucial
but it speeds up the algorithm and reduces the probability of finding
invalid boxes. A range image looks like this:

b. 3D Hough transform
In 2D Hough transform one draws all the possible lines through each
point and calculates the frequency each line is drawn. The most frequent
fields in the Hough table indicate lines that have the most points.
Similarly, in the 3D Hough transform one draws all the planes that go through
each point. As there are infinitely many such planes, we selected
just a few directions that are evenly distributed around the unit
sphere.
One way to do this would be using spherical coordinates. However, this
is not a good idea since it would not give an even sampling of the unit
sphere. We have decided to create directions by starting with the corners
of an icosahedron and dividing all the edges in n parts so that
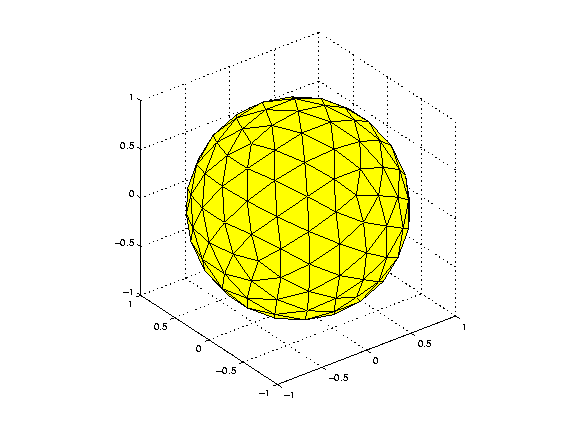
a suitable number of directions is found. The following
two images show an icosahedron and the same icosahedron after dividing
each edge in four parts. This results in 162 directions.

The result of the 3D Hough transform is a table that for each direction
d and each possible distance r contains the number of
points in image that are on a plane which has normal vector (?)
d and which is at the distance r. Thus, in the table
large values indicate good candidates for a plane.
The following image illustrates the Hough table. The white area stands
for strong planes.
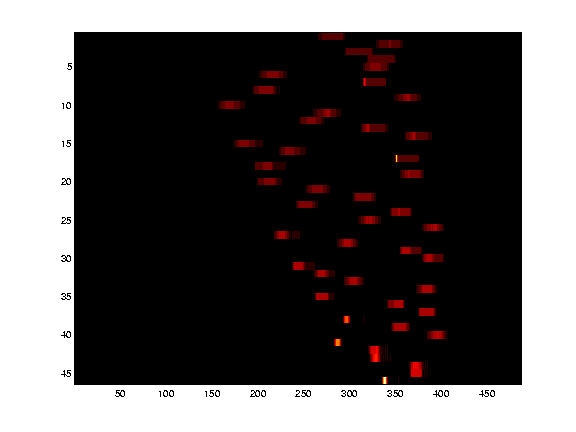
c. Finding orthogonal planes
Next we wish to find the strongest constellation of orthogonal planes.
This would be the nearest corner of a box. Thus, for each orthogonal
constellation of directions we find the strongest planes, build a
triplet table and pick the strongest triplet. The following image
illustrates the triplet table.
d. Finding opposite planes of the box
After finding the strongest triplet constelation of planes, we know
three sides of the box. Now we will have to find the opposite three
planes to fully describe the box. The procedure can be described like
this: The original plane is moved in the normal direction of the plane and
for each displacement position, the number of pixels that lies in the
two orthogonal planes of the box is counted. This creates a profile curve
of the box:
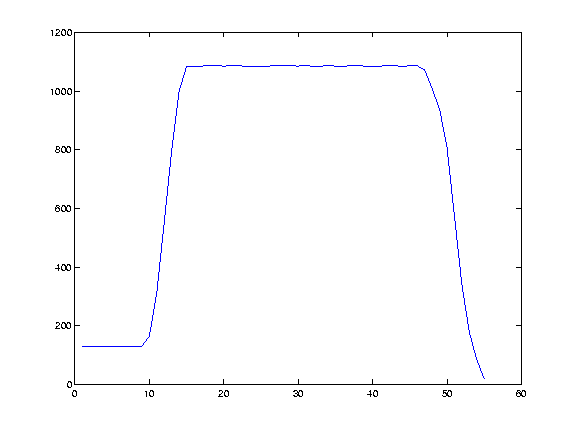
This curve is supposed to have high values when we are inside the box,
and drastically drop when we leave the box. By simply thresholding the
curve the displacement of the original plane that corresponds to the
opposite plane is found. The procedure is repeated for all the three
planes, and we arrive with a complete description of the box.
e. Repeating
The steps c and d are repeated until the stopping criterion
states that no more boxes are found. For example some kind
of a threshold for the triplets could be used as the stopping
criterion.
f. Rendering the 3D scene
In the final step the box is drawn to screen and rotated.
See the
documentation for the rendering program. The result can be
saved as a range image or as ordinary boxes such as the following:

4. Problematic issues with our solution
Our method still has a few points that would need some working on.
The computing time is rather high, the 3D Hough transform is
quite time consuming.
The algorithm also requires that a box has a visible corner with
three visible planes. Very small planes may cause problems.
If two boxes share a common plane, one of them may not be recognized.
If one box occludes another, the size of the occluded box cannot
obviously be decided as the image does not contain sufficient
information for that.








